Curso matplotlib - Gráfico com barras de erros (conjunto de dados)
Figura 1 - Conjunto de dados.

Fonte - pinterest.com.
Para exemplificar como inserir as barras de erros, seguimos utilizando o conjunto de dados de temperatura ao longo do dia da cidade de Birigui, mas agora em 3 dias diferentes:
horario = ['00:00', '02:00', '04:00', '06:00', '08:00', '10:00', '12:00', '14:00', '16:00', '18:00', '20:00', '22:00']
temperatura_13_04_2021 = [21, 19, 19, 18, 23, 27, 31, 33, 34, 28, 23, 26] # temperatura em °C
temperatura_29_04_2021 = [21, 19, 18, 15, 21, 26, 29, 30, 30, 24, 23, 21] # temperatura em °C
temperatura_30_07_2021 = [8, 7, 6, 6, 11, 15, 17, 19, 20, 13, 11, 8] # temperatura em °C
Como as barras de erro se referem a variação dos dados em relação à média, é necessário calcular a média e a variação. Para isto fazer estes cálculos, pode ser utilizada a biblioteca NumPy:
import matplotlib.pyplot as plt
import numpy as np
Para calcular a média da temperatura em cada dia, podemos utilizar o método np.mean(), passando a list com os valores de temperatura medidos ao longo do dia. Como resultado, o método np.mean() retorna a média da list passada.
media_1 = np.mean(temperatura_13_04_2021)
media_2 = np.mean(temperatura_29_04_2021)
media_3 = np.mean(temperatura_30_07_2021)
print(round(media_1,2), round(media_2,2), round(media_3,2))
25.17 23.08 11.75
Agora é necessário calcular uma medida de dispersão. Devido a unidade final ser igual a medida original, é adequado utilizar o desvio padrão como medida de dispersão. Para calcular esta medida, podemos utilizar o método no.std(), onde devemos passar o conjunto de dados e o parâmetro ddof=1. Este parâmetro determina a forma de calculo do desvio padrão. Caso ddof=0 (padrão), o desvio padrão é calculado admitindo que os dados são populacionais. Caso ddof=1, o desvio padrão é calculado admitindo que os dados são amostrais. Como temos apenas 12 medidas de temperatura ao longo de cada dia, os dados são considerados amostrais. Então:
std_1 = np.std(temperatura_13_04_2021, ddof=1)
std_2 = np.std(temperatura_29_04_2021, ddof=1)
std_3 = np.std(temperatura_30_07_2021, ddof=1)
print(round(std_1,2), round(std_2,2), round(std_3,2))
5.56 4.87 5.03
Para facilitar, é criada uma nova variável para a média e outra para o desvio padrão, que armazena os valores dos três dias, como uma sequência, ordenada da data mais antiga, para a data mais recente:
media = [media_1, media_2, media_3]
desv_pad = [std_1, std_2, std_3]
E também uma variável com os nomes dos dias:
dias = ["13/04", "29/04", "30/07"]
Para gerar o gráfico de dispersão, segue-se os passos já vistos anteriormente:
plt.figure(figsize=(8,6))
plt.scatter(dias, media)
plt.show()
Figura 2 - Gráfico de dispersão relacionando a temperatura média na cidade de Birigui-SP em três dias diferentes do ano de 2021.

Contudo, o método plt.scatter() (ou o plt.plot()) não tem um parâmetro para inserir as barras de erro de forma simples. Para inserir uma série de dados contendo as barras de erros, utilizamos o método plt.errorbar() de forma muito semelhante ao que vimos até o momento, que recebe os valores do eixo x, os valores do eixo y. Você encontra maiores detalhes na documentação.
Por exemplo:
plt.figure(figsize=(8,6))
plt.errorbar(dias, media)
plt.show()
Figura 3 - Gráfico de erros relacionando a temperatura média na cidade de Birigui-SP em três dias diferentes do ano de 2021.
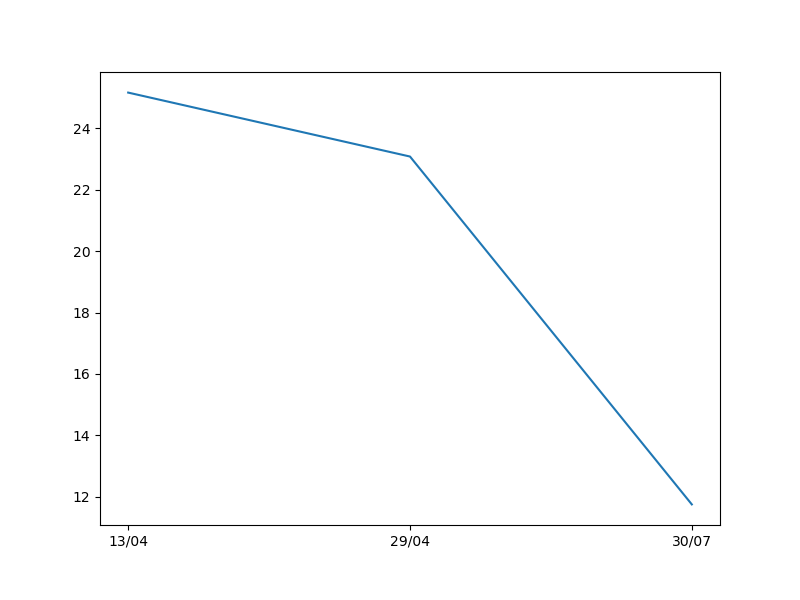
Observe que o resultado obtido é o mesmo que obteríamos caso tivesse sido utilizado o plt.plot(dias, media). Entretanto, agora podemos adicionar as barras de erros, o que não é possível utilizando o plt.plot() ou o plt.scatter().

